🌟 如何理解「自编码器(Auto-encoder)」
自编码器 (Auto-encoder, AE) 是生成式任务里常用的神经网络结构,它会将输入 编码 (encode) 成一段 资料 (latent code) 再 解码 (decode) 到输出,而训练的目标是使它的输入和输出尽可能一致,一般情况下为 无监督训练 (Unsupervised Learning)。我们训练一个 Auto-encoder 往往是希望利用其编码输入信息的能力。
Overview
目前网上大部分关于 Auto-encoder 的文章都是从信号编码的角度讲解的,这么做当然能加深人们对 Auto-encoder 理论基础的理解,但较为晦涩(很多文章用到了不少关于 信号与处理 相关的术语)。
本文的组织如下:
- 先用一个情境类比,对 Auto-encoder 形成直观的理解;
- 介绍 Auto-encoder 的基础内容(结构等);
- 介绍 Auto-encoder 的(早期)作用:为 DNN 训练做初始化;
- 介绍 Auto-encoder 在 CV 领域的基础内容(Unpooling, Deconvolution);
- 简单介绍一些 Auto-encoder 的延伸内容;
情境:你准备专业考试的小抄
设想这么一个情境:你有一门名叫 “云计算” 的专业课因为很难,老师允许大家带一张 A4 版面的小抄去考试。因为考试范围是整本教材的内容,而教材有 600 多页显然不满足考试要求,所以你不得不准备一张固定大小的纸,把整本书的知识点总结到这张纸上,并期望考试的时候通过看这张小抄,回忆起书中的知识,进而通过考试。
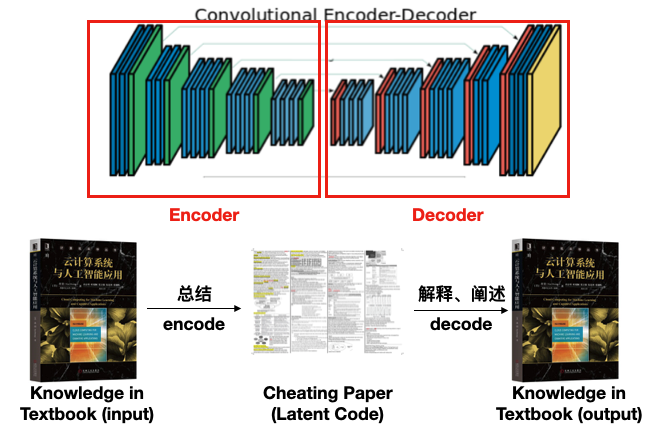
如上图所示,我们可以把考前准备小抄的行为叫做 **编码(Encode)**,把考场上通过小抄回忆出整本书知识的过程叫做 **解码(Decode)**,而这张汇总了整本书精华部分的小抄叫做 隐编码(Latent Code)。对于理智的人来说,我们希望解码出来的内容越接近原教材越好,以减少在考试时犯的错误。
那么我们可不可以把上述 Encode 当作是压缩呢?
这么理解并不恰当,理论上,encode 是比压缩更宽泛的概念,我们可以说压缩是一种 encode,但不会说 encode 是一种压缩。压缩确实对输入信息做了 encode,并且试图以更小的空间尽可能无损地存储输入信息;但 encode 本身并不会在意编码出的信息是否是更小的,甚至可能不在乎信息是否有损耗(如去噪),只是单纯地将信息转化成了目标模型更容易 “解读” 的其它形式而已。
回到刚刚的情境里,压缩往往会使得编码出的信息不可读(所以很多时候我们需要使用压缩软件先解压),而我们希望上述编码过程得到的小抄是可以阅读的。更进一步的,很多时候压缩算法会对全局信息采样,那么解压时也需要先恢复成完整的原始数据;但考试的时候时间紧张,我们希望小抄上有精准的局部内容,不用还原整本书的知识就可以辅助自己作答。
经过四年本科考试的摸爬滚打(training),你已经对准备小抄这事轻车熟路了:你知道小抄空间金贵,哪些东西该记哪些可以不记,哪些内容如何表述才不会产生歧义;你也知道小抄做完之后最好再解读一遍看看和原文有多大差别,确定这个细微差别不会影响考试发挥;你甚至还学会了如何划分小抄上的空间方便自己快速定位内容;有时由于以前学过的课程和这门考试也相关,你只需一些简单的调整就能快速地记录/唤起知识点。
你做好了小抄,并且找来这门课往年的卷子做模考(test)——模考成绩还不错。你把这个好消息告诉给了好朋友小深,小深看到你模考成绩不错,和你说他来不及准备小抄了,能不能直接复印你的小抄去考试用,你欣然答应了。
小深也不是糊涂虫,在正式考试前还是拿你的小抄做了一下模考,直接裂开 🤯。
因为两个人的背景、基础(甚至大脑结构)不同,他看你的小抄就跟看天书一样,模考考得稀烂。他现在有几个选择:
1. 像你一样从头开始做小抄;
2. 在你的监督下读懂小抄的内容,尤其是你做小抄的思路和使用的符号;
3. 根据自己的理解调整小抄上的内容来应付考试。
小深自觉时间不多了来不及从头再完整看一遍教材,于是选择了方案 3,推敲你小抄上符号的含义,并根据线索在教材里查找个别他还不知道的内容,再根据自己的实际情况修订自己复印来的小抄。
经过反复练习,他也把自己的小抄做好了,并且在考试里考得还不错。比起方案 1 的从头开始,小深说你的小抄帮他节省了不少时间,他少走了很多弯路。
你的另一个朋友小迁选了一门与云计算相近的课叫 “分布式与并行计算”。小迁是时间管理大师,整天做一些和自己专业不相干的事,但厉害在她都能胜任并做得还不错。这天她问你要了云计算的小抄,说自己也没时间准备了打算拿这份小抄去准备并行计算的考试,而且云计算的范围涵盖了并行计算这门课的知识点,小迁觉得完全可行。
你将信将疑地把小抄给了小迁。出乎你意料的是,小迁这家伙竟然一个字没动,硬是用你的云计算小抄通过了并行计算的测验。小迁说她本身迁移学习的能力比较强,她就拿你的小抄硬怼大量并行计算的练习题,主动调整自己的思维模式来适应将来的考试。她还笑眯眯地说,以后和你借小抄应该都看得懂了😎。
这个情境直观地演示了 Auto-encoder 的基本概念、特点及应用场景,下面我将用相对严谨和学术的方式再捋一遍 Auto-encoder。
AE Basics
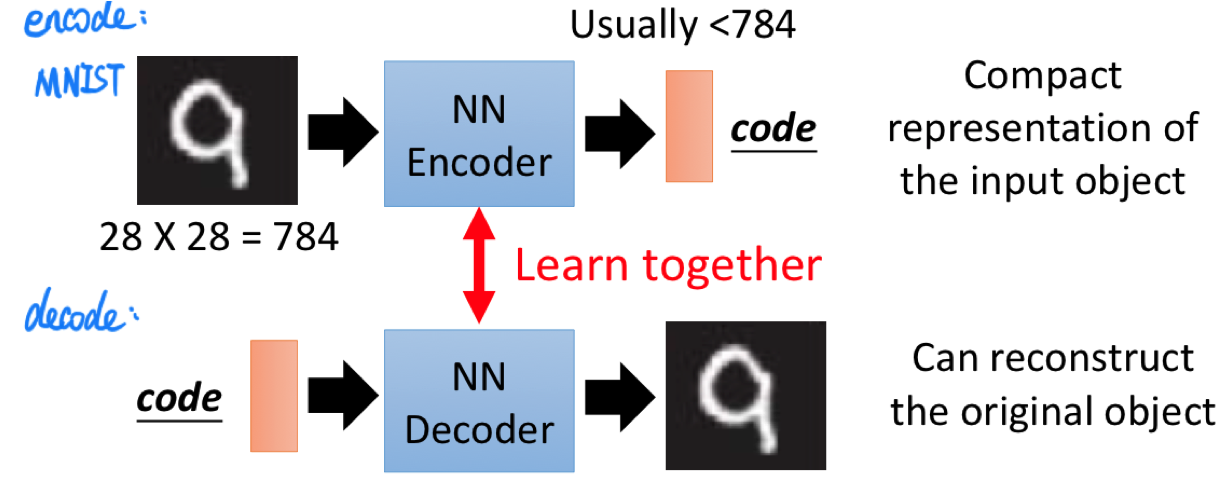
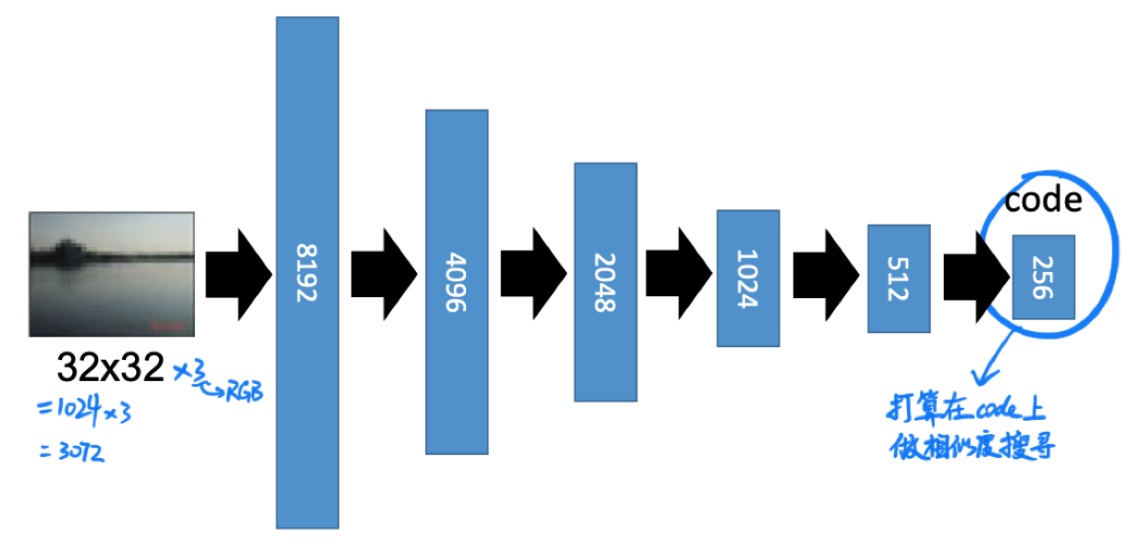
在如上图所示的例子中,Encoder 将输入(MNIST 图片,$28 \times 28=784$ 维)编码成一段 code,这个 code 的维度一般小于 784,相当于是对原始输入的 compact representation;同时我们还有一个 Decoder,这个 Decoder 接收一个 code 作为输入,并试图将这段 compact representation 所蕴藏的信息重建出来。
遗憾的是,由于很难设计 Loss Function,Encoder 和 Decoder 很难单独训练,于是我们把两个网络接起来一块训练,期望整个网络的输入尽可能地等于输出。这就会让人想到 PCA:
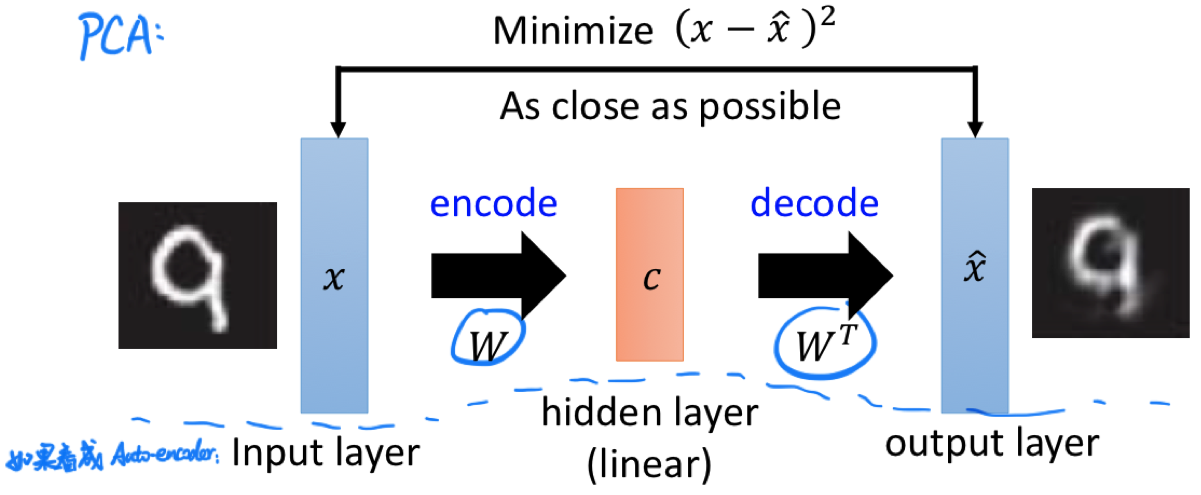
如果我们用人工神经网络来实现类似的结构,把层数叠多再做一些调整,我们就可以得到如下 Deep Auto-encoder 的结构:
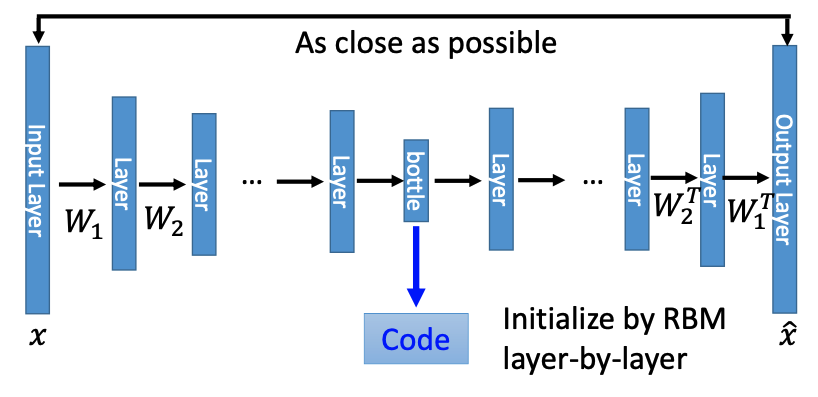
训练 Deep Auto-encoder 时,我们的目标是让网络的输入 $x$ 和输出 $\hat{x}$ 尽可能地相近,而这个过程并不需要任何的 label 信息,所以是 无监督学习(Unsupervised Learning),训练的过程会调整 $W_1, W_2, …, W_m$ 的值。理论上让 code 左右两侧的参数对称(如 $W_1$ 和 $W_1^T$)是不必要的,但这样的设计可以减少一半的训练参数量,也可以减少模型过拟合的可能性。除此之外,在当年要训练这样的一个深度网络,还需要使用 RBM 的方法进行初始化,这里就不展开细讲了。
AE for DNN Pre-training
Auto-encoder 的一个早期应用在于为深度神经网络的参数做初始化。
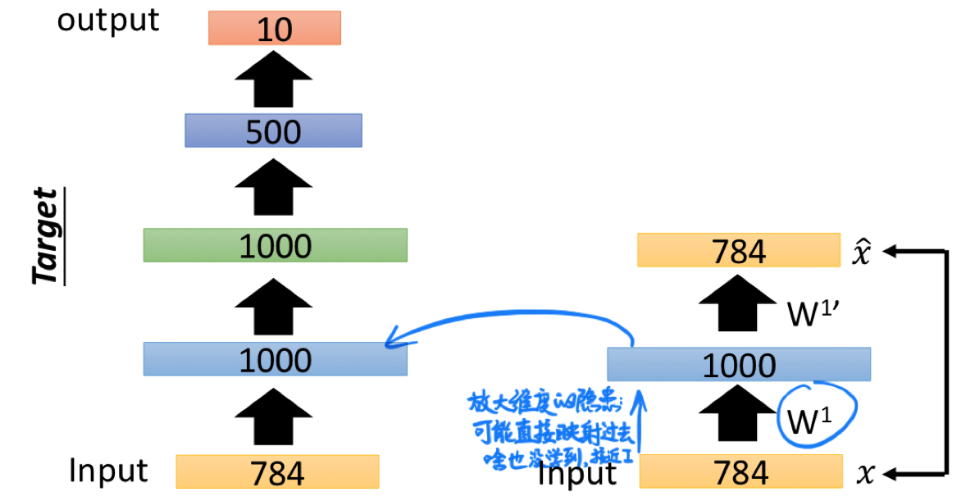
如上图左半部分所示,我们的目标是设计一个 (784 -> 1000 -> 1000 -> 500 -> 10) 的 DNN 来做 MNIST 的手写数字分类。
在以前如果随机初始化参数直接训练这样的网络往往会很难收敛。于是,我们可以先设计一个如上图右半部分所示的 Auto-encoder,将其自监督训练至收敛,保留 (784 -> 1000) 的参数 $W^1$。此时我们认为 $W^1$ 起到了 encoder 的作用:将 Input 的特征信息抽取到了 1000 个维度上。
一般而言,不推荐在设计 Auto-encoder 时把 code 的维度放大到比输入输出还大。这是因为网络很有可能会 “偷懒” 而直接把输入映射到输出上,最后啥也没学到,得出一个接近 Identity Matrix 的矩阵。如果非要增大维度,可以在训练的时候增加 regularization 规范参数的分布。
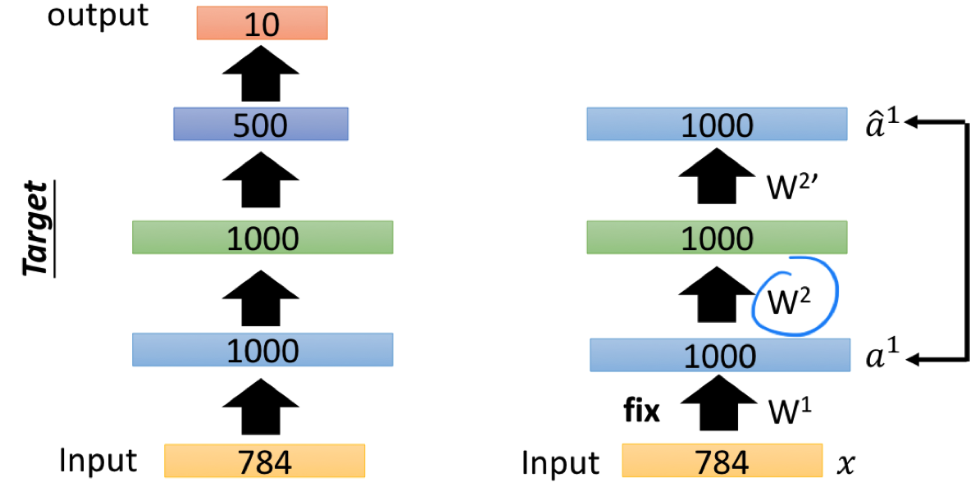
接着,我们丢弃右侧 (1000 -> 784) 的部分,比照左侧的网络结构在右侧接上 (1000 -> 1000),固定住 $W^1$ 的值,训练 (1000 -> 1000 -> 1000) 这个 Auto-encoder。
需要注意的是,训练时我们仍然传入 MNIST 的图片 $x$,但控制 $L_1$ 层的输出 $a^1$ 与 $L_3$ 层的输出 $\hat{a^1}$ 尽可能一致(而不是让 $x$ 与其它哪层的输出尽可能一致)。
收敛后,我们得到参数 $W^2$。
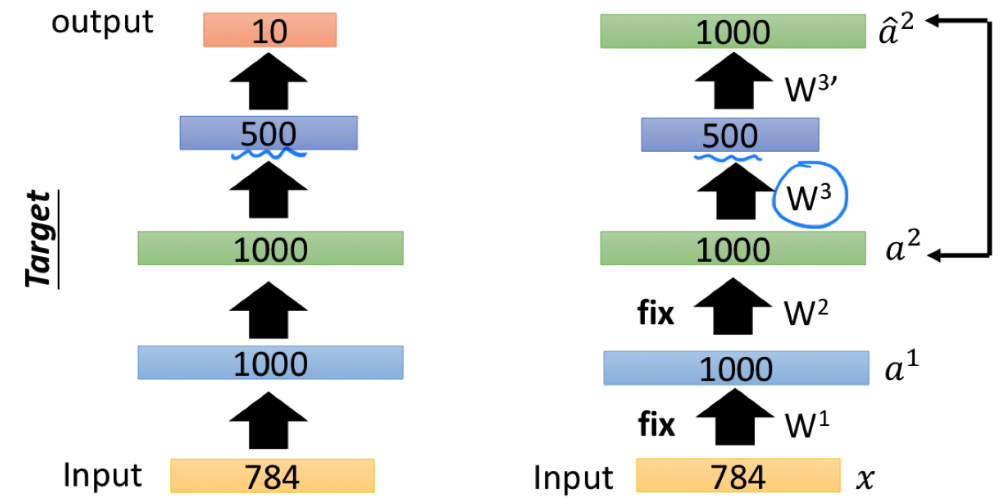
然后,我们重复类似的操作,固定住 $W^1$ 和 $W^2$,训练得到 (1000 -> 500) 的 Encoder 参数 $W^3$。
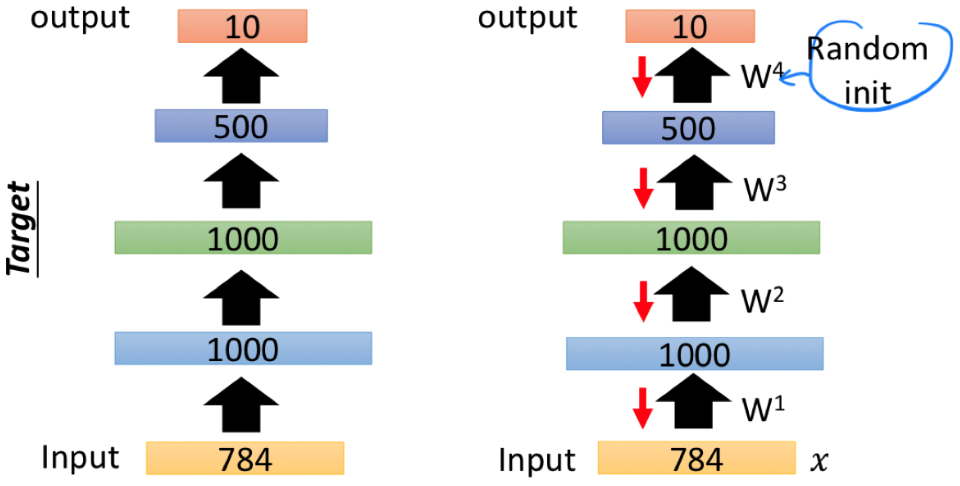
最后,我们随机初始化 (500 -> 10) 的参数 $W^4$,并允许 $W^1$、$W^2$、$W^3$、$W^4$ 随 backpropagation 更新,就可以使用形如 (Input Image, Label Digit) 的 pair 进行训练了,而这就得到了我们想要的 target network。
在以前 training 技术没那么好的时候,要训练一个 DNN 几乎都要这样的 pre-training。在现在的情况下,如果说本身训练集很小(label 很少),我们也可以用这样的方法对网络参数进行比较好的初始化。
AE for CNN
前面只是提到了 Auto-encoder 的大体框架,下面我们来进一步了解 Auto-encoder 在实际 计算机视觉(CV) 任务中的结构。
Searching Similar Images
在 CV 中一个常见的任务是 “以图搜图”。举例来说,假设我们有一张 Micheal Jackson 的照片但不知道他的名字,而我们想在网络上去搜寻相似的图片,那么我们会期望搜索引擎接收我们上传的图片作为参考来搜索相似的图片。
那么如何判断两张图片相似呢?
第一种方式就是直接计算两张图片 像素层面上的相似度(Distance in pixel intensity space),比如算两张照片像素矩阵之间的内积,或直接算它们之间的欧氏距离。

可以看到通过这种方式检索出来的图片的确颜色及颜色的分布是相似的,但它们的内容却与我们想要的结果大相径庭。
按照前面对 Auto-encoder 的理解,我们认为 latent code 充分抽取了输入图片的高维特征,那么我们能不能直接通过计算不同 code 之间的相似度来判断图片的相似度呢?
如果可以的话,我们预期的 Encoder 会是这个样子的:
在 CV 中抽取特征最常用的就是由 Convolution Layer 和 Pooling Layer 交替叠出的网络结构,考虑到 Auto-encoder 沿 code 两侧对称的特性,那么一个使用了 CNN 的 Auto-encoder 会长这样:
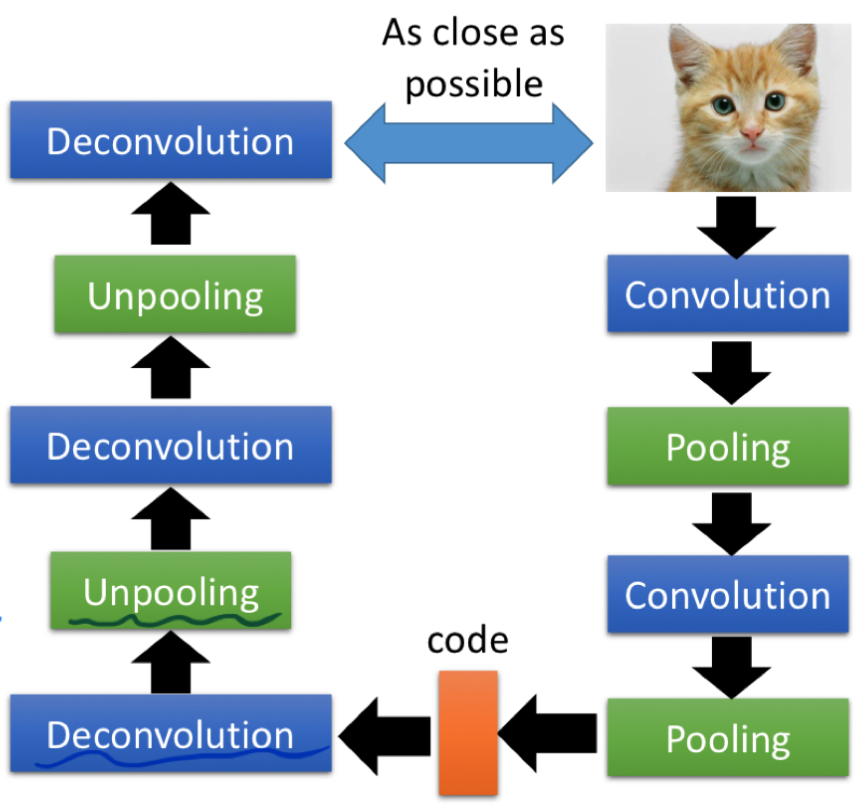
现在我们有了一个绝妙的想法,就差程序员了这里的问题是,如何设计 Decovolution 和 Unpooling 模块呢?
Unpooling Layer
Unpooling 有很多种不同的方法,这里只介绍其中比较常用的两种。
![Pooling [Left] and Unpooling [Right]. Reference: https://leonardoaraujosantos.gitbooks.io/artificialinteligence/content/image_segmentation.html](/zh-hans/2021/03/10/%E5%A6%82%E4%BD%95%E7%90%86%E8%A7%A3-Auto-encoder/Unpooling.png)
第一种方式是在 Max Pooling 的时候记下每个最大值的位置(称之为 “Max Locations Switches”),在 Unpooling 的时候对非最大值的位置补 0。
如上图所示,我们将一个 $4 \times 4$ 的 Rectified Feature Map 池化为 $2 \times 2$ 的 Pooled Map 时,记下每个子区域中最大值的位置(图中灰色的部分)。当要对这个 Pooled Map 进行 Unpooling 时,我们通过查找 Max Locations Switches,把最大值的颜色的位置还原,其余地方(图中黑色的部分)补 0 (也就是这个通道上没有 intensity)。
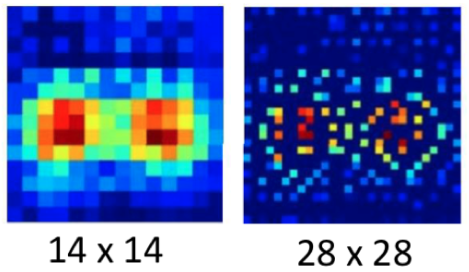
上图是一个将 $14 \times 14$ Feature Map 给 Unpooling 成 $28 \times 28$ 的例子。
另一个替换方案是将 Max Locations Switches 都抛弃,直接对 Unpooling 后的 Map 按子区域填充该区域的最大值。
Deconvolution Layer
实际上 Deconvolution 本质上还是用 Convolution 实现的。我们先来看看卷积的过程,这里以一维的卷积举例方便理解。
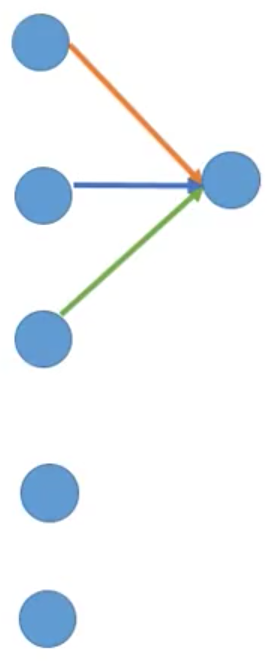
如上图所示,这是一个 input size=5 的一维向量。我们设 kernel size=3,那么做一次卷积相当于对这个 input 不同位置的值乘上不同的系数(橙、蓝、绿色的箭头分别代表不同的系数)再相加起来。
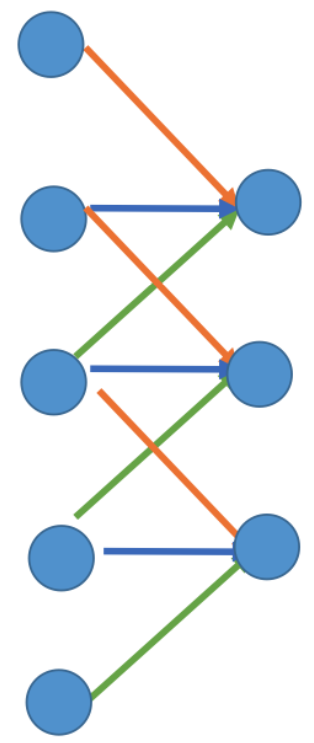
当 kernel 遍历完 input 之后,将输出一个 size=3 的向量,其计算结果如上图所示。
那么,想当然的,我们希望一个对应的 deconvolution 能实现将每个值还原回卷积前的输入,也就是下图的效果(注意箭头方向):
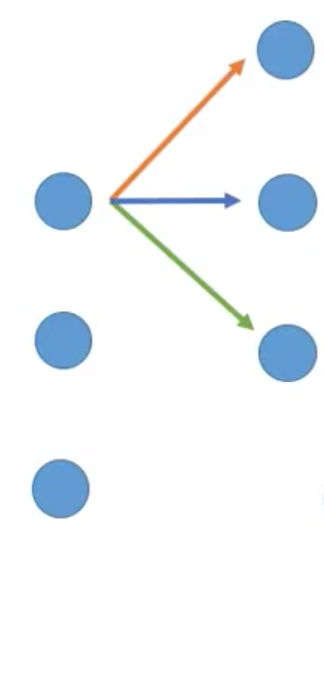
遍历完成后,我们会得到:
<img src=”Deconvolution-4.png”style=”zoom:25%;” />
现在我们引入一个非常巧妙的设计,给要被 decovolution 的 code 加一些值为 0 的 padding,并直接对其进行卷积计算:

由于 0 乘任何数都得 0,所以上述的计算结果可以看作是只有橙色箭头的计算真正起了作用。
当卷积完成时:
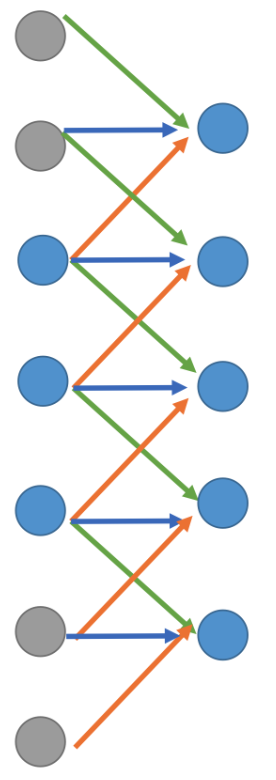
我们对比一下我们期望的 deconvolution 和现在完成的 convolution:
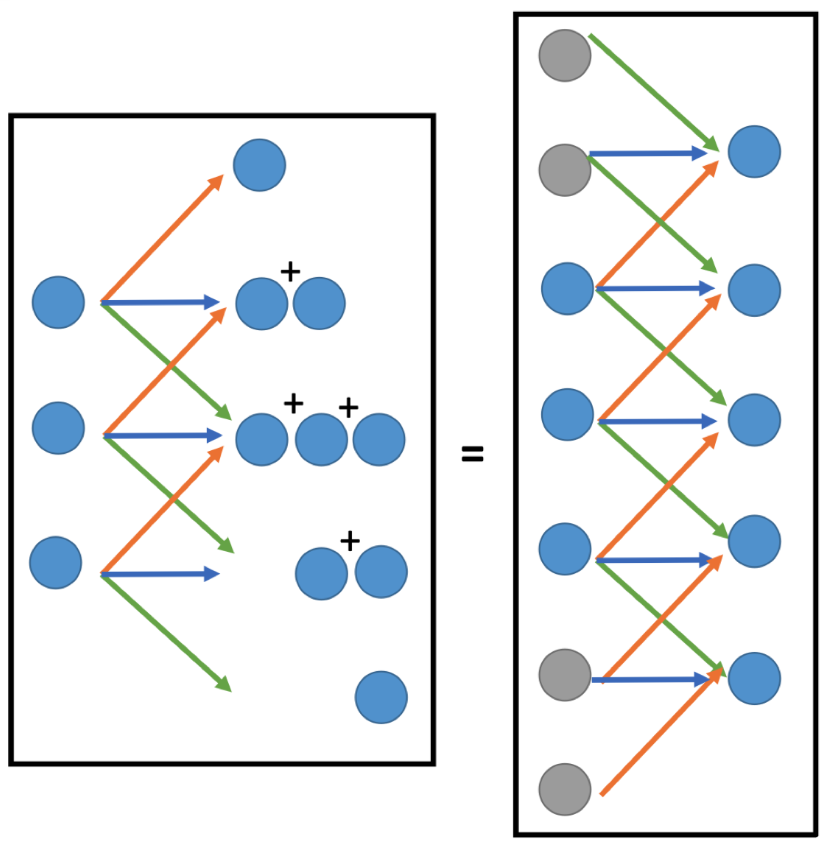
会发现,它们做的操作是完全一样的!也就是说,deconvolution 可以通过先 padding 再做 convolution 实现,两者本质上是等价的(所以你在 CNN Auto-encoder 的代码里看到的 decoder 也是由卷积层的接口实现的)。
现在通过训练这个 Auto-encoder,我们用编码的 256 维 latent code 来做相似度计算,检索出来的结果如下:

可以看出,使用 lantent code 做检索不光节省了计算资源(维度从 3072 维降到了 256 维),而且效果还更好(起码检索出来的都是人脸)。
Further Research on AE
De-noising Auto-Encoder (DAE)
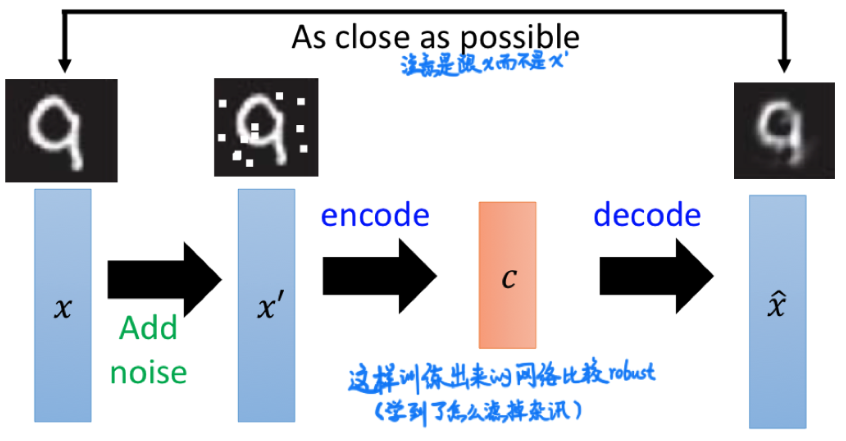
为了让 encoder 更加 robust 一些(避免过拟合),我们可以在 input 上添加随机噪声再输入到要训练的 encoder。注意训练 DAE 时仍是把输出 $\hat{x}$ 和原始输入 $x$ 接在一起,而不是和被噪声污染的 $x’$ 接在一起。这样训练出来的 encoder 有去掉杂讯的能力。
How to evaluate an encoder?
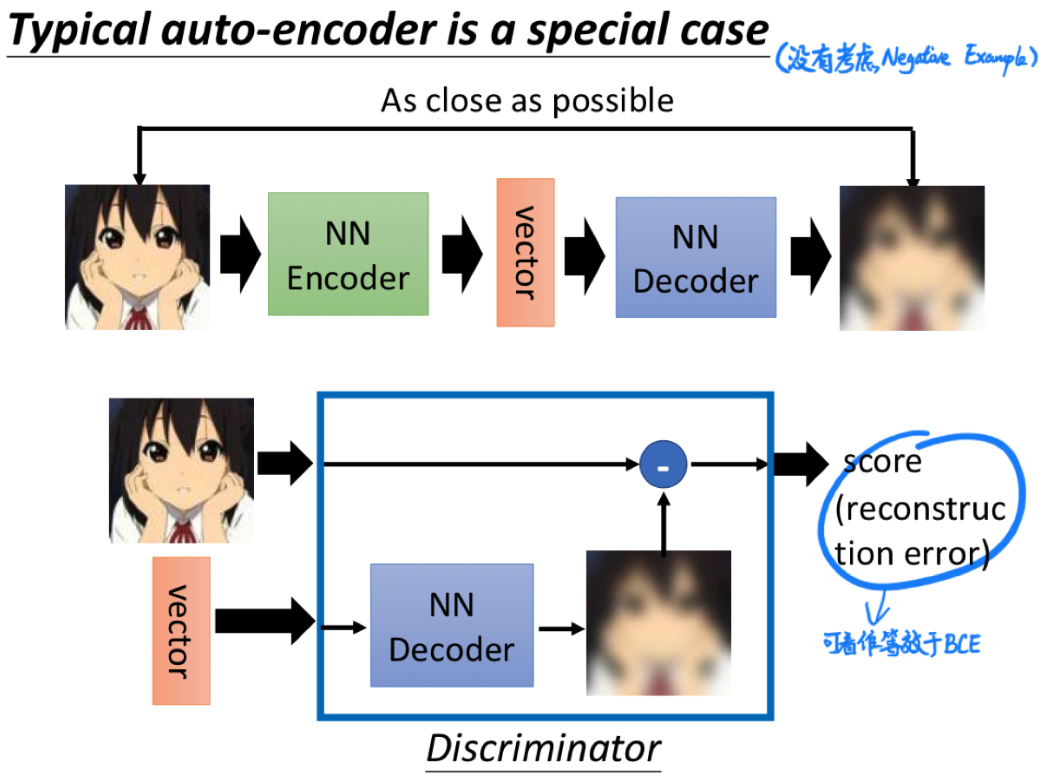
除了 Reconstruction Error 之外,我们还有没有别的方式来衡量一个 Encoder 的好坏呢?我们可以认为,一个 Encoder 越好,说明其编码信息(尤其是捕捉特点)的能力越强,越不同的源数据编码出的 embedding code 越不像。
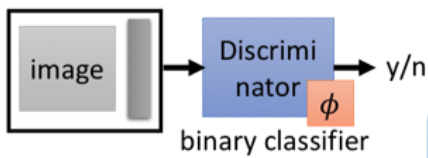
现在我们给出一张 Image 和一段 code 作为一组输入,传入一个训练好的 Binary Classifier 中,如果这个 Image 和 Embedding code 是一对,则输出 Y,否则输出 N。
这样的 Classifier 也很好训练,只需要设成 Binary Cross Entropy Loss (BCE) 并投喂一些正负样本就可以训练了:
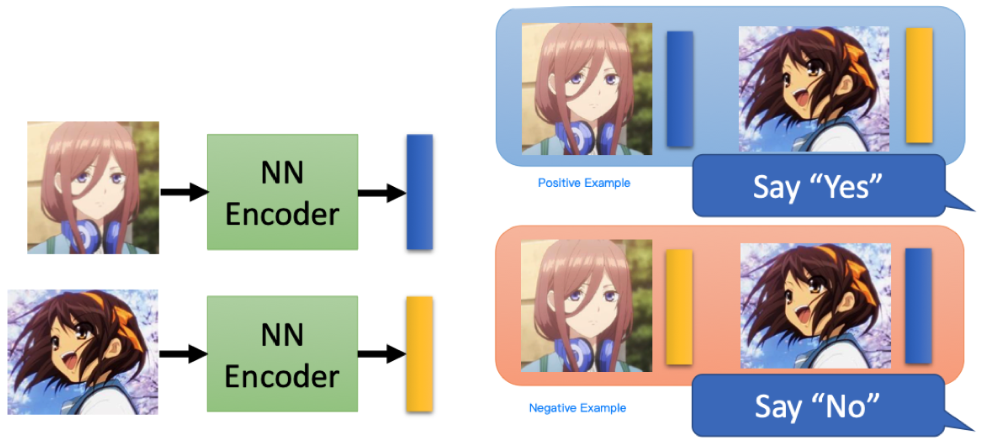
在我们定义好 Classifier 的 Loss function $L_D$ (在这里是 BCE)后,我们训练 Classifier 的参数 $\phi$ 来获得最优值 $L_D^*$。
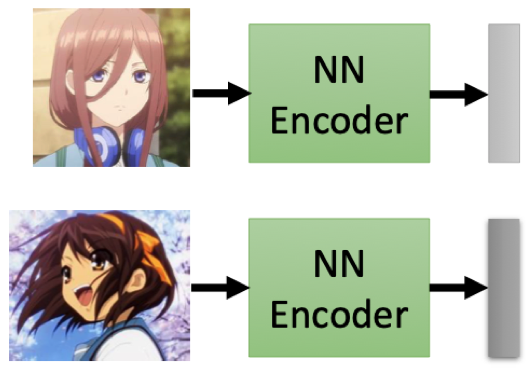
上图所示的 Encoder 对不同图片编码出的 embedding code 很相似,这将会使得 Classifier 最后收敛时的 $L_D^*$ 很大:

换句话说,如果我们想要训练好一个 Encoder,我们应该优化 Encoder 的参数 $\theta$ 使 $L_D^*$ 尽可能小。将上述式子代入得:

也就是说,我们可以通过优化 Classifier 的 Loss 来优化 Encoder。
从这个角度看,经典的 Auto-encoder 只是一种没有考虑负样本的特殊形式:
Acknowledge
本文的脉络和图片资源主要参考了 李宏毅老師的相關課程,并加以自己的理解和报告内容所写,如有错误望不吝赐教。